Rotating Workforce Scheduling in MiniZinc DRAFT
Workforce scheduling is a classical optimization problem. Improved schedules can be better both for the workers and for the business, but are often surprisingly hard to find. One common variant of scheduling is called Rotating Workforce Scheduling (shortened as RWS), and is sometimes called cyclic scheduling. In RWS, a weekly schedule is created for a group of workers covering the projected needs. Each worker will rotate through the schedule, working all different weeks.
Solving RWS is a challenging problem, both for manual and automatic approaches. This post will describe developing a reasonably realistic variant of finding an RWS schedule using MiniZinc. Starting with the basic structure and then adding more and more typical requirements to get realistic schedules.
What is a rotating schedule?
What does it mean to rotate through a schedule? If there are employees, then different weekly schedules are created. Each employee follows one week-schedule, and every week all employees shift to the next schedule in the rotation. This ensures fairness: everyone eventually experiences each schedule pattern. Using this type of schedule is useful for cases where there is a variety of requirements, usually involving work outside of normal office hours.
In this post we will keep to a fairly simple model that is still realistic, with D day shifts, E evening shifts, N night shifts, and finally · off days.
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | E | E | E | E | · | · | · |
| 2 | D | D | D | · | · | D | D |
| 3 | D | · | · | N | N | N | N |
| 4 | · | · | · | · | E | E | E |
| 5 | D | D | D | D | D | · | · |
| 6 | N | N | N | N | N | · | · |
| 7 | N | N | N | · | · | D | D |
Use the week buttons above to see how each employee’s schedule changes as the rotation progresses.
There are many cases where the scheduling needs are for more detailed levels, not just three types of shifts. Still, this level of detail is often usable, and will allow us to reason about the problem at a simple level.
A basic MiniZinc model
First we will look at a basic model that handles the data, the instances, and the basic constraints and printing. In the next section, we will add the constraints for the labor rules to turn a basic schedule into something that could be used in practice.1
Problem Domain
The first step in writing a MiniZinc model is to set up the data-definitions. There are three axis that are needed, the days, the employees, and the shifts.
enum Days = {Mon, Tue, Wed, Thu, Fri, Sat, Sun};set of Days: Weekend = {Sat, Sun};
enum ShiftsAndOff = {Day, Evening, Night, Off};set of ShiftsAndOff: Shifts = {Day, Evening, Night};In the above code, the days are named as an enum.
A separate set of days for a weekend is also defined, as that will be needed in some constraints.
While {Sat, Sun} could be used directly in the code it is better to have it named.
The enum ShiftsAndOff represent all the types of shifts (day, evening, and night) as well as off days.
A subset Shifts is defined from this with just the shifts.2
Data and instance
Each scheduling problem includes some data that defines the problem.
int: employees;set of int: Employees = 1..employees;
array[Days, Shifts] of int: requirements;The employees integer tells us the number of employees, while the requirements
matrix tells us the number of people needed for working a shift on each weekday.
In the model the Employees will correspond to one week schedule each.
The rotation among employees is something that is done with the result of the model.
The number of employees and the requirements are defined in a data-file. The following data will be used as the running example.
employees = 7;requirements = [| 3, 1, 2 | % Mon: 3 Day, 1 Evening, 2 Night 2, 1, 2 | % Tue: 2 Day, 1 Evening, 2 Night 2, 1, 2 | % Wed: 2 Day, 1 Evening, 2 Night 1, 1, 2 | % Thu: 1 Day, 1 Evening, 2 Night 1, 1, 2 | % Fri: 1 Day, 1 Evening, 2 Night 1, 1, 2 | % Sat: 1 Day, 1 Evening, 2 Night 1, 1, 2 | % Sun: 1 Day, 1 Evening, 2 Night|];Variables and meeting requirements
The most important part of defining a constraint programming model is usually deciding on a viewpoint. That means deciding what variables will be used to describe a solution to the problem. Here we will use a straight-forward viewpoint, with a Shift variable for each day and employee.
% The actual schedulearray[Days, Employees] of var ShiftsAndOff: schedule;
% Rolled out schedule with the first week repeatedarray[int] of var ShiftsAndOff: repeated_schedule = [schedule[day, employee] | employee in Employees, day in Days] ++ schedule[.., 1];The schedule array maps each day and employee to a variable shift.
Some constraints will go over different weeks for more global properties.
Since this is rotating workforce scheduling, the first week will follow the last week.
The repeated_schedule array of variables is defined with the first employee’s week
repeated again at the end, unrolled into one single sequence.
This makes it easier to state these rules that have properties that go across weeks.
Note that if any of the constraints were over longer periods than one week,
more than one week would need to be added.
As an example, consider the following unrealistic schedule and
the unrolled repeated schedule where the first row is repeated at the end.
| N | N | N |
| E | E | E |
| D | D | D |
| · | · | · |
| N | N | N | E | E | E | D | D | D | · | · | · | N | N | N |
% Requirements met for each dayconstraint forall (day in Days) ( global_cardinality(schedule[day, ..], Shifts, requirements[day, ..], requirements[day, ..]));The core (and only) constraint for the basic model is that for each day of the week the right
number of people needs to work each shift.
The global_cardinality constraint
is made for counting the number of occurences of different values.
In this case, there is one such constraint per day where the count of each of the different shifts scheduled
are set to be at least as much as the requirement, and at most as much as the requirement.
Since not all employees will work in a day, the remaining employees will be scheduled as Off,
the only ShiftsAndOff member that is not limited.
Solving and printing solutions
The only remaining part is to indicate that this is a satisfaction problem and to print a solution.
solve satisfy;
function string: shift2string(ShiftsAndOff: shift) = if shift = Day then "☀️" elseif shift = Evening then "🌆" elseif shift = Night then "🌃" elseif shift = Off then " " % Double space to match emojis endif;
output [ concat(day in Days) ( shift2string(fix(schedule[day, employee])) ) ++ "\n" | employee in Employees];Using solve satisfy; means that any valid solution is ok, there is no objective to optimize.
The printing function will give a visual example of how the schedule looks like.
Running this model in the MiniZinc IDE version 2.9.4
with the Gecode solver and statistics added gives the following output.
🌃🌃🌃🌃🌆🌃🌃🌃🌃🌃🌃☀️🌆🌆🌃🌃🌃🌃☀️☀️☀️🌆🌆🌆🌆☀️☀️☀️☀️☀️☀️☀️----------%%%mzn-stat: failures=0%%%mzn-stat: initTime=0.00355504%%%mzn-stat: nodes=33%%%mzn-stat: peakDepth=32%%%mzn-stat: propagations=64%%%mzn-stat: propagators=7%%%mzn-stat: restarts=0%%%mzn-stat: solutions=1%%%mzn-stat: solveTime=0.000760917%%%mzn-stat: variables=49%%%mzn-stat-end%%%mzn-stat: nSolutions=1%%%mzn-stat-endFinished in 141msec.This solution can be visualized using the same solution visualizer as above.
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | · | · | · | · | · | · | · |
| 2 | N | · | · | · | · | · | · |
| 3 | N | N | N | · | · | · | · |
| 4 | E | N | N | N | N | N | N |
| 5 | D | E | E | N | N | N | N |
| 6 | D | D | D | E | E | E | E |
| 7 | D | D | D | D | D | D | D |
The solution meets the resource requirements, but it is not a usable schedule. Most of the work is in one long chunk without resting days, and there is no consideration for weekends or for how to handle night work.
From the statistics, we can see that there are 7 propagators, which is one global constraint propagator for each day. The search is backtrack free (no failures), since it is easy to construct the schedule. The solve time is less than a millisecond.
Adding rules
As mentioned above, the schedule produced with the basic model is not actually usable. In this section, additional rules for schedules will be added one by one.
Consecutive Days Off Each Week
A common requirement in many jurisdictions is that employees should get two consecutive days off each calendar week. This can be added as a constraint for each week.
% At least 2 consecutive days off each weekconstraint forall (employee in Employees) ( regular(schedule[.., employee], ".* Off Off .*"));The regular constraint
was originally introduced in order to handle scheduling patterns3.
The constraint is defined using Finite Automata4,
which can be generated from regular expressions.
Here we are using the MiniZinc version that accepts a string with a regular expression.
These strings can include enum names, and use the . character for wild-cards and * for repetitions 0 or more times.
The string ".* Off Off .*" means that the week will start with zero or more days with anything scheduled,
then at some point there will be two Off days, then zero or more additional days.
Or in other words, each week contains at least two consecutive Off days.
Running with this constraint gives us a new result.
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | N | · | N | N | · | · | · |
| 2 | N | N | N | N | · | · | · |
| 3 | E | N | E | E | N | · | · |
| 4 | D | E | D | · | · | N | N |
| 5 | · | · | D | D | N | N | N |
| 6 | D | D | · | · | E | E | E |
| 7 | D | D | · | · | D | D | D |
This is starting to look a lot more reasonable. Each week has some time off, and therefore the maximum length of time worked is a lot less. The statistics show that there are now some backtracks, but still not very many. The solve time is still in the milliseconds range.
%%%mzn-stat: failures=50%%%mzn-stat: initTime=0.00362304%%%mzn-stat: nodes=127%%%mzn-stat: peakDepth=26%%%mzn-stat: propagations=994%%%mzn-stat: propagators=14%%%mzn-stat: restarts=0%%%mzn-stat: solutions=1%%%mzn-stat: solveTime=0.00120338%%%mzn-stat: variables=49%%%mzn-stat-end%%%mzn-stat: nSolutions=1%%%mzn-stat-endFinished in 180msec.Maximum Days Without Rest
One thing that can be seen in the previous solution is that sometimes there are runs where an employee will work for seven days in a row. One common restriction for many areas is to limit the maximum number of days in a row that work is scheduled. Here we will use the limit of 5, so that at most five days in a row are scheduled. Note that while both the previous rule and this rule enforce a certain amount of time off, they are complementary and non-dominating. There are schedules that satisfy one rule but not the other, and vice versa.
% At most five days without restconstraint let { array[int] of var bool: off_days = [d = Off | d in repeated_schedule] } in sliding_sum(1, 6, 6, off_days);The first step is to create a set of auxiliary Boolean variables off_days that indicate if a certain day is an off day.
This is done for the repeated_schedule in order to not have a schedule with the first five days with work and the last five days in the
last week with work.
The sliding_sum constraint is used to enforce that
in each consecutive subsequence of a certain length, the sum of values is within a certain range.
Here, in each subsequence of length 6, the sum must be in the range , so there is at least one day that is an off day.5
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | · | · | N | N | · | · | · |
| 2 | N | N | N | N | N | · | · |
| 3 | N | N | E | E | N | · | · |
| 4 | E | E | D | · | · | N | N |
| 5 | D | D | D | · | · | N | N |
| 6 | D | D | · | · | E | E | E |
| 7 | D | · | · | D | D | D | D |
This version of the schedule looks a lot more reasonable just in the shape of working and off days. There is time off every week, and there is never more than 5 days of work. The statistics show that there are now significantly more backtracks, but the solve time is in the tens of milliseconds range.
%%%mzn-stat: failures=2213%%%mzn-stat: initTime=0.00567179%%%mzn-stat: nodes=4455%%%mzn-stat: peakDepth=29%%%mzn-stat: propagations=2364985%%%mzn-stat: propagators=267%%%mzn-stat: restarts=0%%%mzn-stat: solutions=1%%%mzn-stat: solveTime=0.0558184%%%mzn-stat: variables=202%%%mzn-stat-end%%%mzn-stat: nSolutions=1%%%mzn-stat-endFinished in 292msec.Weekend Rest Requirements
There is one remaining obvious problem with the off days in the schedule: all the working weekends are clustered. One common rule is that workers will need at least one out of every 3 weekends off.
% At least 1 out of 3 weekends off.constraint let { array[Employees] of var bool: free_weekend = [ forall (day in Weekend) ( schedule[day, employee] == Off ) | employee in Employees]; } in sliding_sum(1, 3, 3, free_weekend ++ free_weekend);We will use a similar technique as above with auxiliary variables,
but here the variables will represent if a weekend is free.
The definition of that is that both the days of the weekend for that employee / row in the schedule
has Off in the schedule.
Another sliding_sum constraint is used for sub-sequences of length 3, ensuring at least one weekend is rest.
One interesting difference is that the constraint is over free_weekend ++ free_weekend since
this constraint needs to see three weeks at a time and needs selected information for some days.
The repeated_schedule is not usable here.
It is an unrolled schedule, which would make it harder to extract weekends.
In addition, it would need more than one extra week at the end.
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | · | N | N | N | · | · | · |
| 2 | N | N | N | N | N | · | · |
| 3 | N | E | E | · | · | N | N |
| 4 | E | D | D | · | · | N | N |
| 5 | D | D | D | · | N | · | · |
| 6 | D | · | · | E | E | E | E |
| 7 | D | · | · | D | D | D | D |
Looking at the weekends, this schedule is starting to look ok. The off days are in a decent pattern in general. Looking at the statistics, the number of failures and the time is roughly the same as before.
%%%mzn-stat: failures=2424%%%mzn-stat: initTime=0.00581904%%%mzn-stat: nodes=4875%%%mzn-stat: peakDepth=29%%%mzn-stat: propagations=1731964%%%mzn-stat: propagators=316%%%mzn-stat: restarts=0%%%mzn-stat: solutions=1%%%mzn-stat: solveTime=0.0416498%%%mzn-stat: variables=229%%%mzn-stat-end%%%mzn-stat: nSolutions=1%%%mzn-stat-endFinished in 226msec.Night Shift Limits
The most important part left that makes the schedule bad is that there is no consideration for rest around night shifts. Night shifts are taxing and require rest. We will follow a common restriction that night shifts are only allowed when there is rest both before and after. In addition, a maximum of three night shifts in a row are allowed.
The above (deterministic) finite state automaton represents the allowed transitions between days.
Starting in the O state, everything is ok the next day.
For day and evening shifts, the next state is the DE state, where everything except night shifts are ok (with off shifts going back to O).
From the O state, night shifts can be assigned.
The N1, N2, and N3 states are used as counters for how many night shifts have been assigned, and after the third one there must be a rest day.
% At most 2 night-shifts in a row, and then restconstraint let { set of int: States = 1..5; int: start_state = 1; array[States, ShiftsAndOff] of opt States: transitions = array2d(States, ShiftsAndOff, [| % D E N O 2, 2, 3, 1 | % State 1, base case, off time 2, 2, <>, 1 | % State 2, base case, day and night shifts <>, <>, 4, 1 | % State 3, 1 night shift: if off go to state 1, if night go to state 2, else fail <>, <>, 5, 1 | % State 4, 2 night shift: if off go to state 1, if night go to state 3, else fail <>, <>, <>, 1 | % State 5, 3 night shifts: if off go to state 1, all others fail |]); } in regular(repeated_schedule, transitions, start_state, States);The state machine can be expressed in MiniZinc as the state transtition table.
It goes over the States and the values, with either the next state or none (<>) if there is no transition for that value in that state.
Adding this constraint gives us the following schedule.
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | N | · | · | D | D | D | D |
| 2 | D | · | N | N | N | · | · |
| 3 | D | E | E | E | E | · | · |
| 4 | N | N | N | · | · | E | E |
| 5 | D | D | D | · | · | N | N |
| 6 | · | N | · | N | N | · | · |
| 7 | E | D | D | · | · | N | N |
This schedule is quite realistic, with typical major scheduling rules taken into consideration. Again using Gecode and the standard search, there are not that many failures and the search time is quite low.
%%%mzn-stat: failures=286%%%mzn-stat: initTime=0.00224604%%%mzn-stat: nodes=593%%%mzn-stat: peakDepth=27%%%mzn-stat: propagations=250354%%%mzn-stat: propagators=428%%%mzn-stat: restarts=0%%%mzn-stat: solutions=1%%%mzn-stat: solveTime=0.0104299%%%mzn-stat: variables=285%%%mzn-stat-end%%%mzn-stat: nSolutions=1%%%mzn-stat-endFinished in 185msec.Benchmarking the model
Testing a model on just one instance is not that interesting. The model here is an updated version of one that I developed for a poster at Stockholm Optimization Days 2022. For that poster, I generated a benchmark set with employees from 5 to 30, with 10 instances for each size. In total, there are 70 instances. Making a rotating schedule for 30 employees at once is not that common, but it is still useful to measure how different solvers behave at different sizes. For background on how to benchmark a MiniZinc program, see On Benchmarking MiniZinc and the LinkedIn Queens Problem.
All tests are run using MiniZinc 2.9.4 on a Mac M1 Max with 64 GiB of memory. We will test the following solvers
- Gecode 6.3.0, a traditional CP solver
- OR-Tools 9.14, a Lazy Clause Generation portfolio solver
- Chuffed 0.13.2, a Lazy Clasue Generation solver
- COIN CBC (2.10.12/1.17.10), an older MIP solver
- HiGHS (1.1.0), a modern MIP solver
- Huub 0.1.0, a Lazy Clause Generation solver
- Pumpkin 0.1, a Lazy Clause Generation solver
Each solver is run with a time-out of 60 seconds. All solvers are tested both single-threaded and with 10 threads with free search enabled. Note that CBC was excluded from the multi-threaded testing, as it interpreted the time-out to be based on user time and not wall-clock time.
For testing, you can download the full MiniZinc model as well as the example instance and the full set of benchmark instances.
Cactus plots 🌵
As the main comparison, we will look at cactus plots. These plots show how many instances can be solved in a cumulative time, with the time plotted on a log scale.
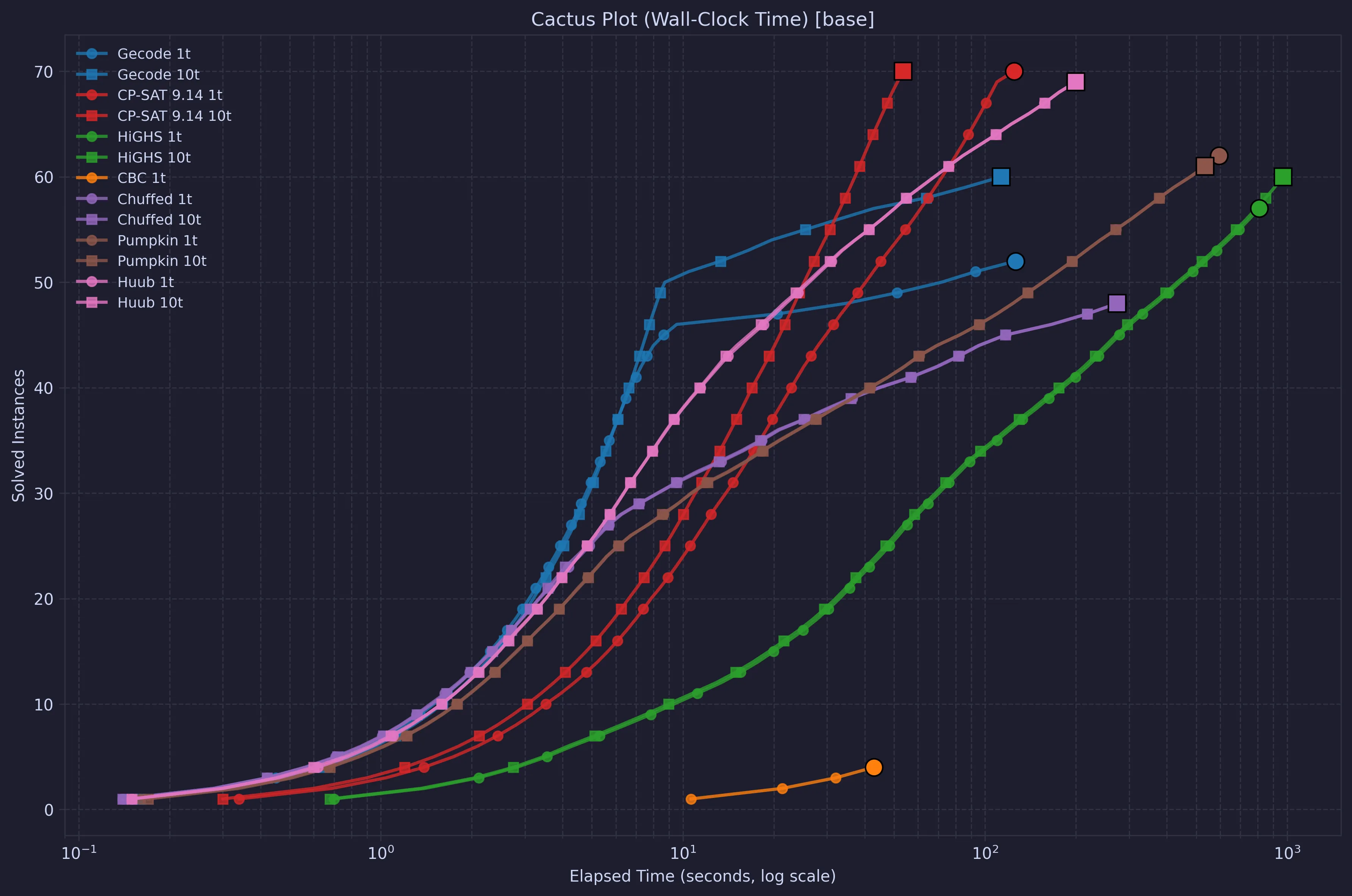
In this plot, we can see that Gecode is quite fast for the simple problems. However, after a while OR-Tools CP-SAT catches up and wins handily. COIN-OR CBC only solved a few instances, so it is not really interesting for this model. HiGHS, as a representative of modern MIP solvers was apart from CBC the slowest solver, although in the end it solved more than Chuffed and single-threaded Gecode. In previous experiments, I’ve seen that the automaton for night shift limits seems to be tricky for MIP solvers. It is interesting to note that Huub, while being quite a new solver, did almost as well as CP-SAT.
The above graph looks at total wall-clock time to run each solver, including translation from MiniZinc. This plot looks instead only at the self-reported solve times from the solvers.
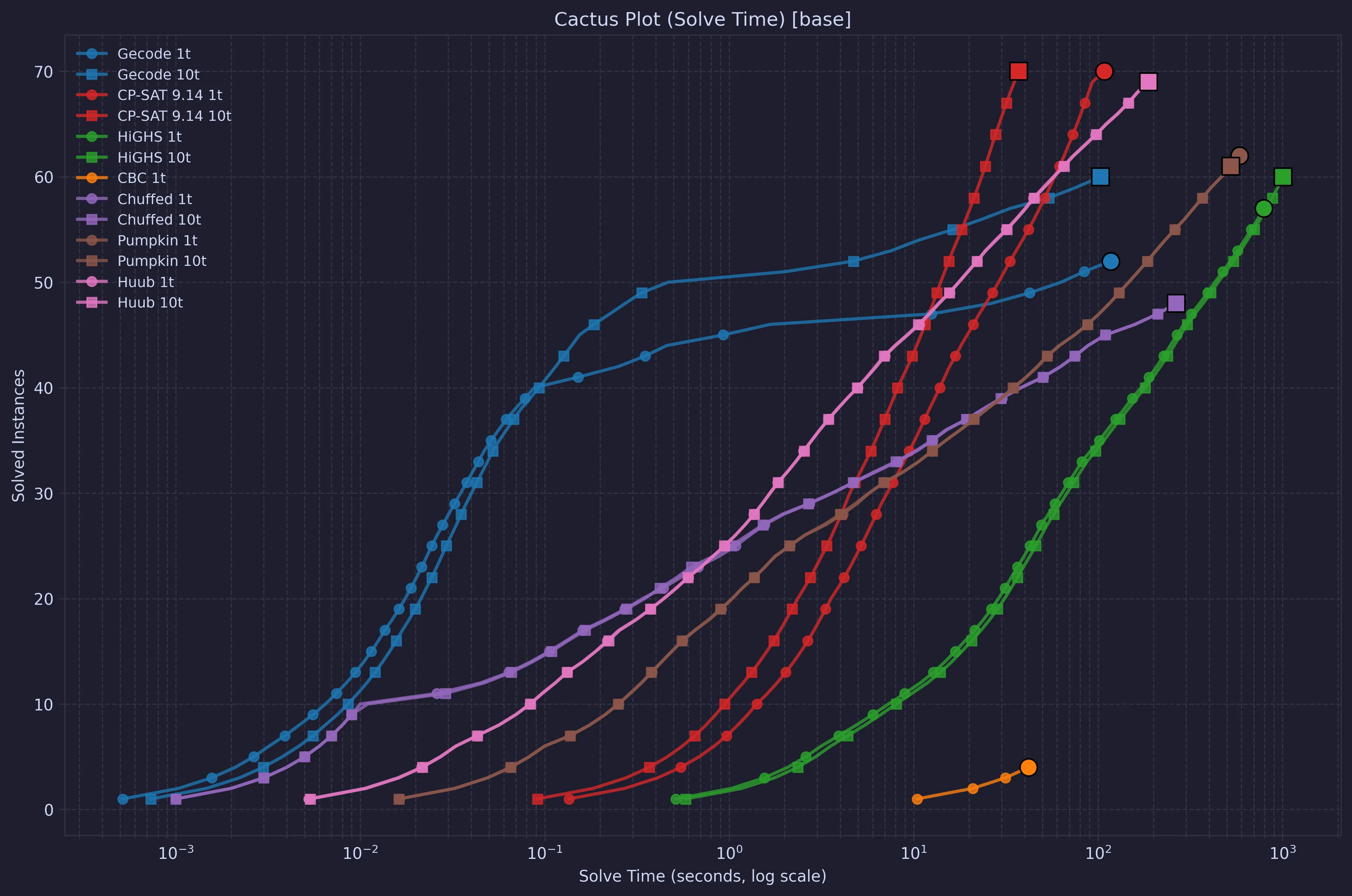
The main take-away is that Gecode is quite fast for the simple problems, while OR-Tools CP-SAT is slower to get started but better in total. These differences in the starting phase are “hidden” by the common cost of translating from MiniZinc in the wall clock time plot.
Run time vs number of employees
It is natural to think that the run-times will change depending on the number of employees. In this plot, the run-times are summed for each employee count, and plotted. Time-outs are counted as the full 60 seconds, and the opacity of the lines is set by the amount of solved instances.
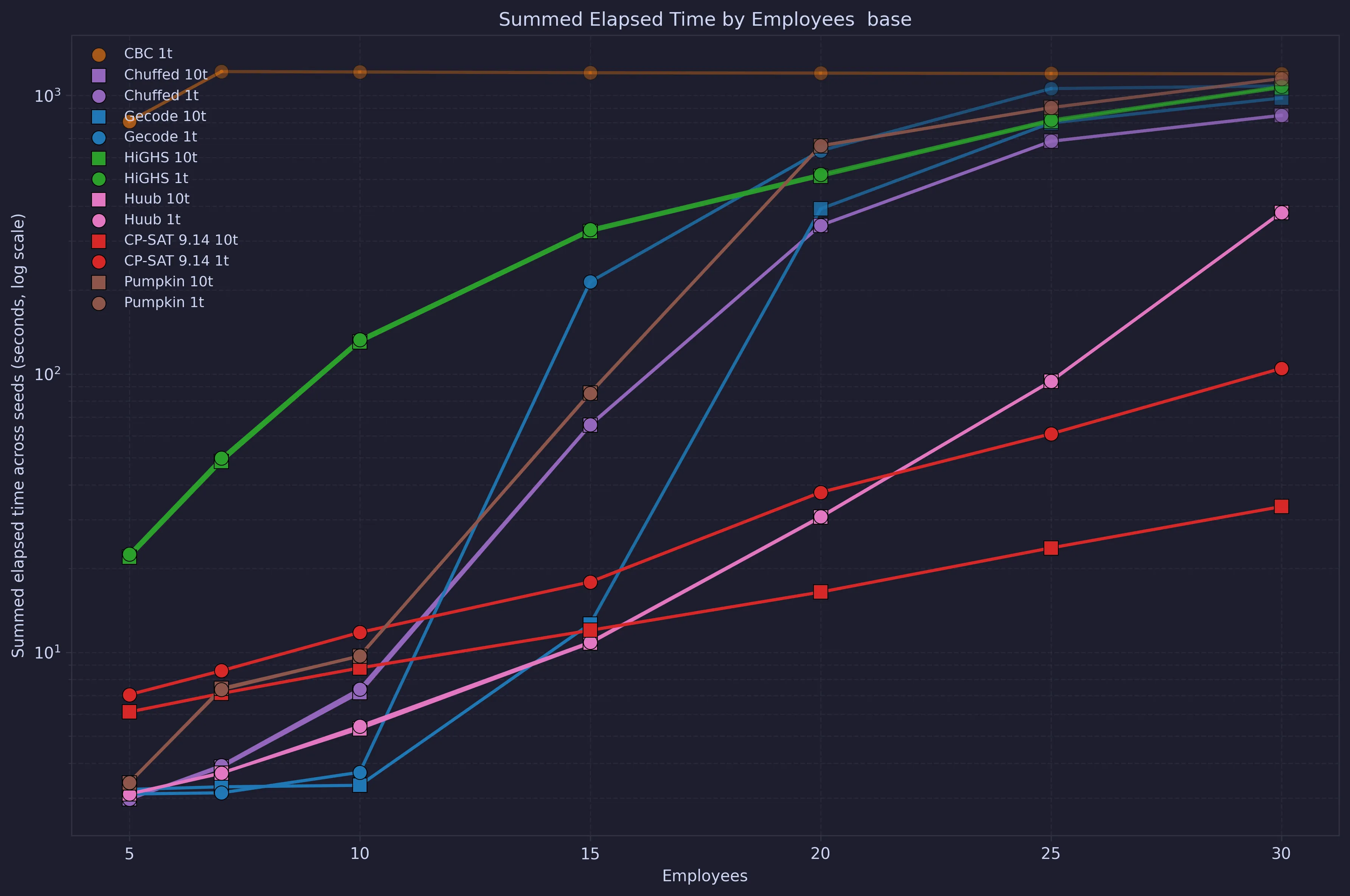
From this, we can see that above 15 employees, CP-SAT with 10 threads looks like a clear winner. If we instead take the average of solved instances, the view is slightly different.
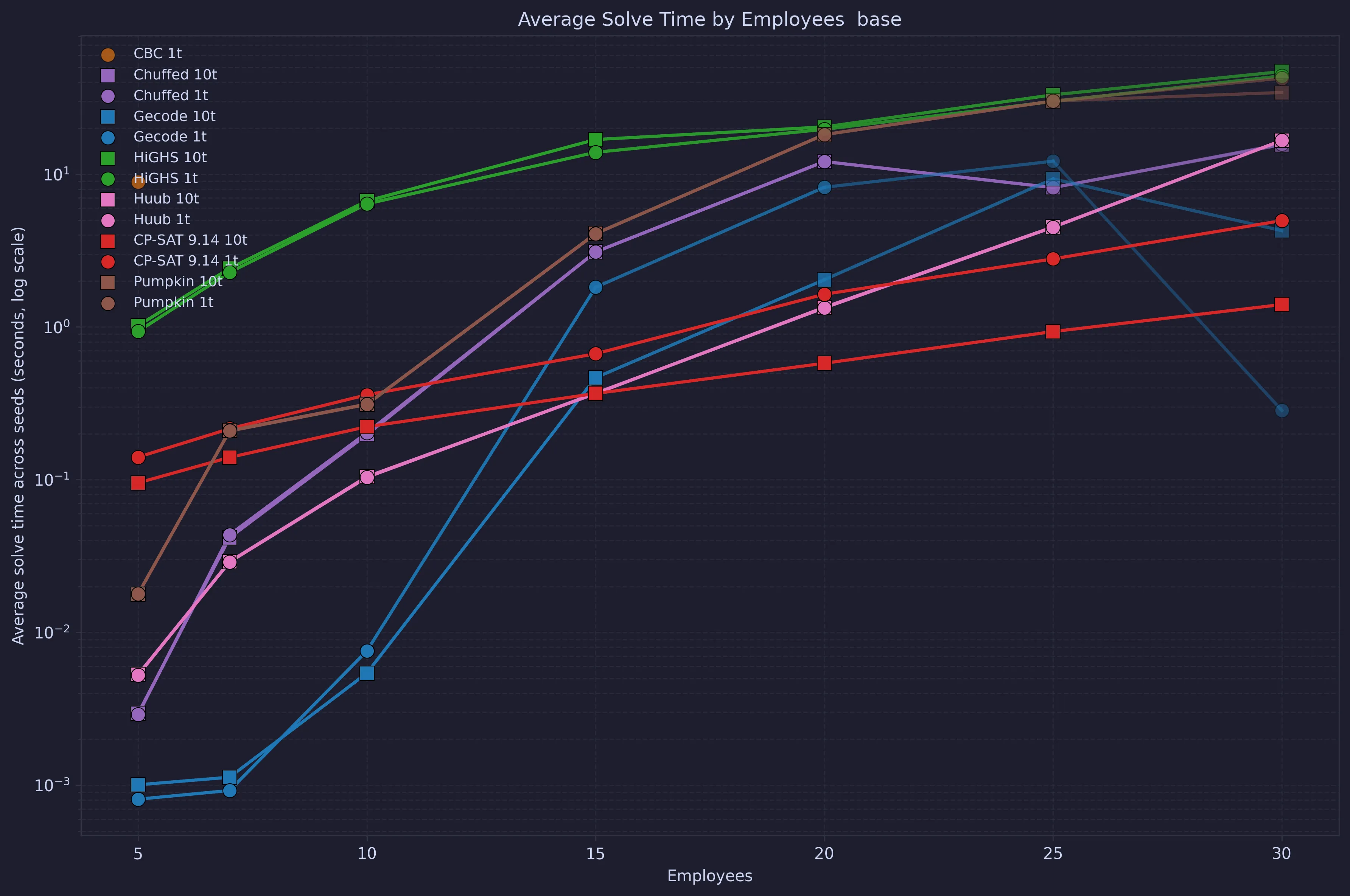
What is interesting to note here is that for the instances that are solved Gecode is surprisingly efficient for large instances. This might be a selection effect (only the simple cases are solved), but it might also indicate that the right heuristic could be very useful.
OR-Tools CP-SAT version
As was argued in The Work Task Variation Problem, the development of CP-SAT has made significant improvements. That difference was for optimization problems, while this version of RWS is a satisfaction problem. To test the historical development, three older versions of OR-Tools CP-SAT are tested against the current version.
- 9.14 (current version, June 2025)
- 9.12 (February 2025)
- 9.7 (August, 2023)
- 9.3 (March, 2022)
First lets look at the cactus plots
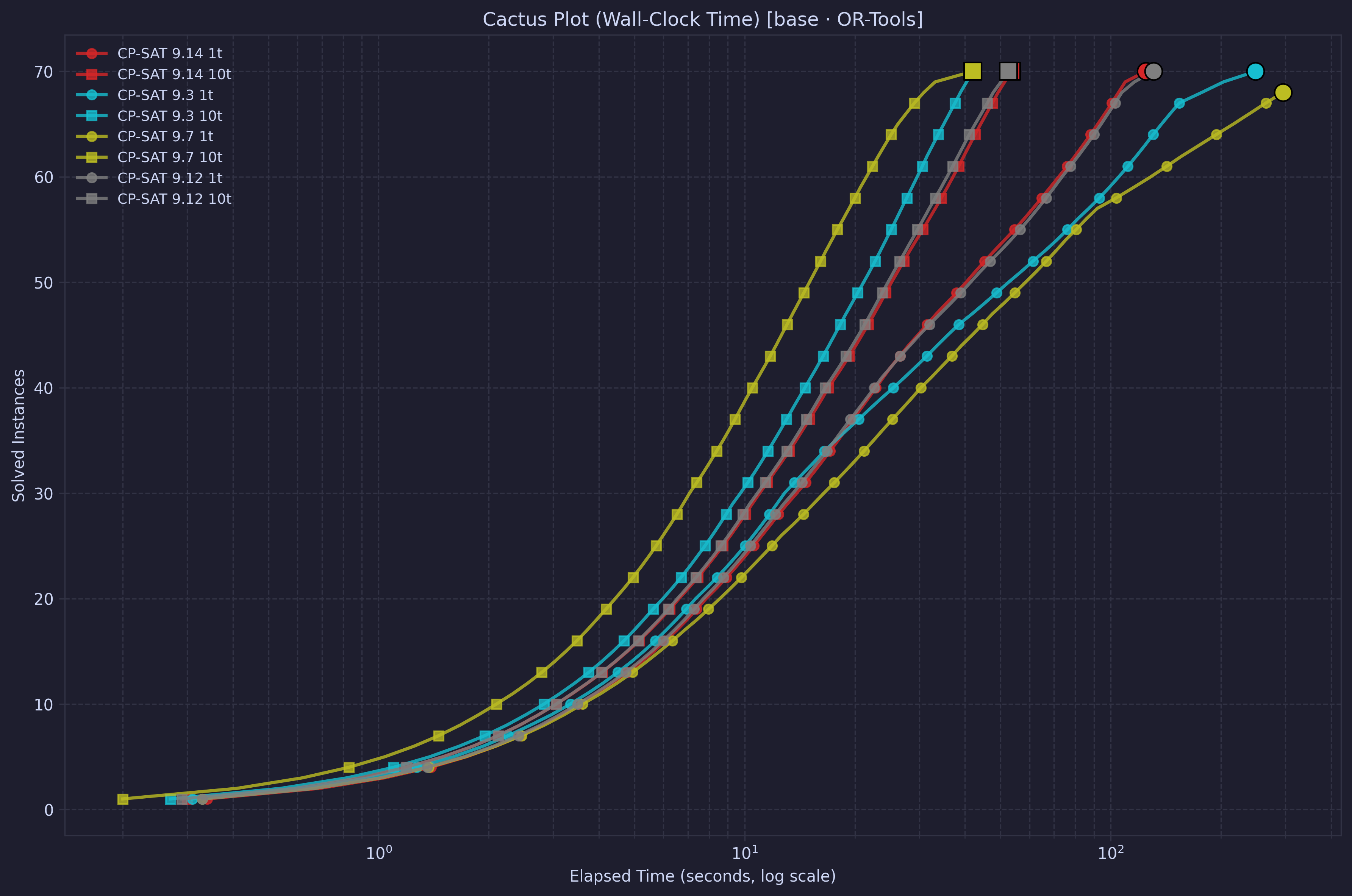
It’s interesting to see that version 9.14 for this fairly simple problem is slightly slower in the multi-threaded version than the 9.3 and 9.7. At the same time, it is slightly faster in the single-threaded configuration. It is also very similar to version 9.12.
Looking at the performance based on the number of employees, we can see that although the cactus plot for version 9.7 with 10 threads looked better, the slope is worse. This means that the newer version, while slower in general, seems to be more robust in solving the problem over different sizes.
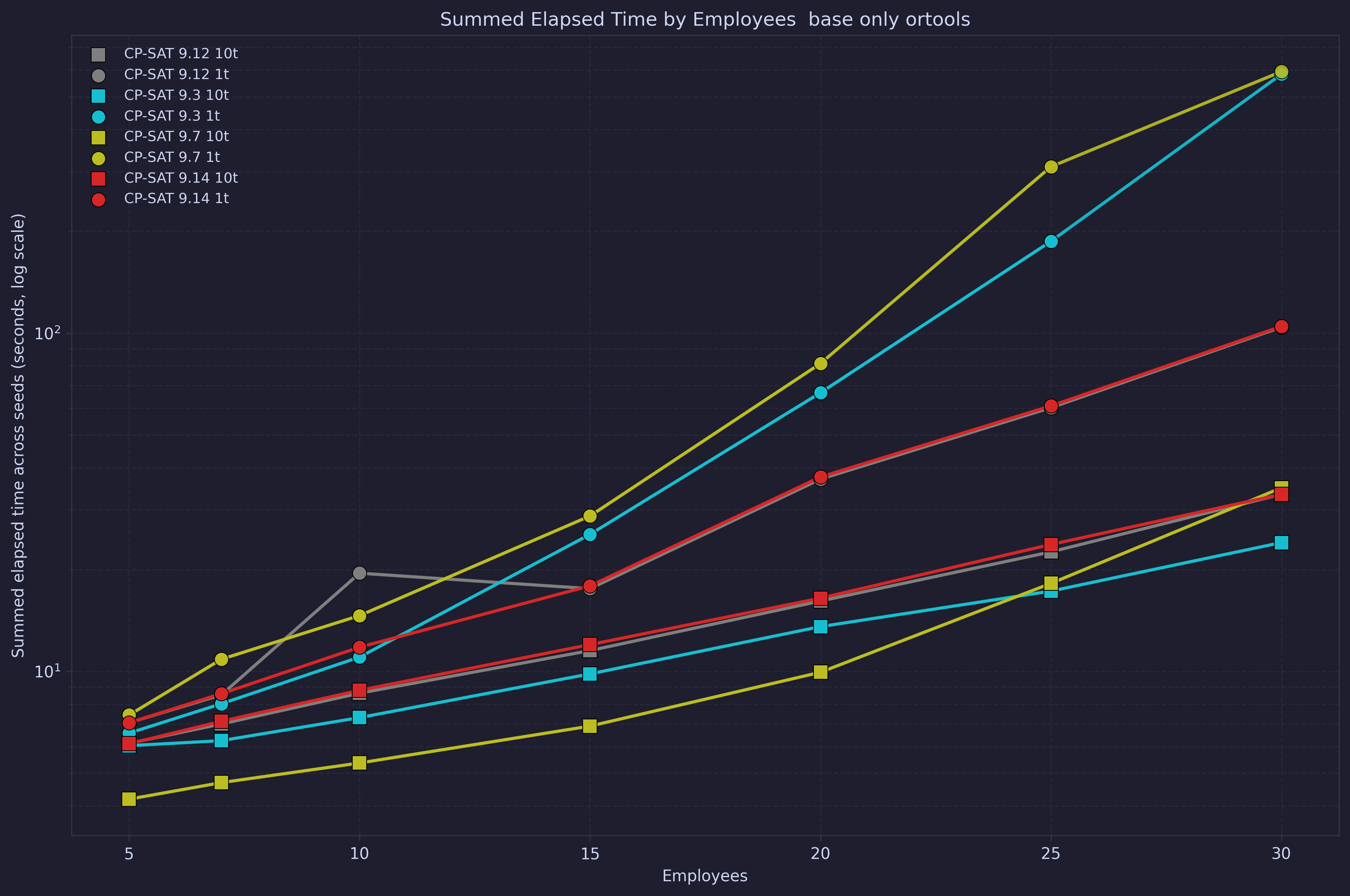
Custom Search Strategy
All of the above tests are made with a simple solve satisfy; statement.
However, it is also possible to specify search annotations in MiniZinc.
There are more constraints over the weekends than there are over weekdays, and there are also more constraints over night shifts than over day and evening shifts. Therefore, it seems likely that it would be a good idea to assign shifts on weekends first, and to focus on night shifts first. A search specification would look like this.
array[ShiftsAndOff] of int: reorder = [3, 2, 1, 4];
solve :: int_search( [reorder[schedule[day, employee]] | employee in Employees, day in Weekend ], input_order, indomain_min)satisfy;The above code collects all the weekend-days, and asks the solver to assign them in order. By re-mapping the enum values to known integers, we can make sure that night shifts are tried first, then evening and day, and the last to be tested is off days. Note that this annotation is only for some of the days, not the full schedule, the remaining variables will be assigned using the default strategy of the solver.
| # | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| 1 | D | D | D | · | · | N | N |
| 2 | N | · | · | D | D | E | E |
| 3 | D | · | N | N | N | · | · |
| 4 | N | N | N | · | · | D | D |
| 5 | D | D | D | · | · | N | N |
| 6 | · | N | · | N | N | · | · |
| 7 | E | E | E | E | E | · | · |
Unfortunately, this turned out not to be a good idea. Gecode is a traditional CP solver, and as such it gains the most from good search annotations. However, in the below cactus plot and time for different employees, we can see that it is in general worse.
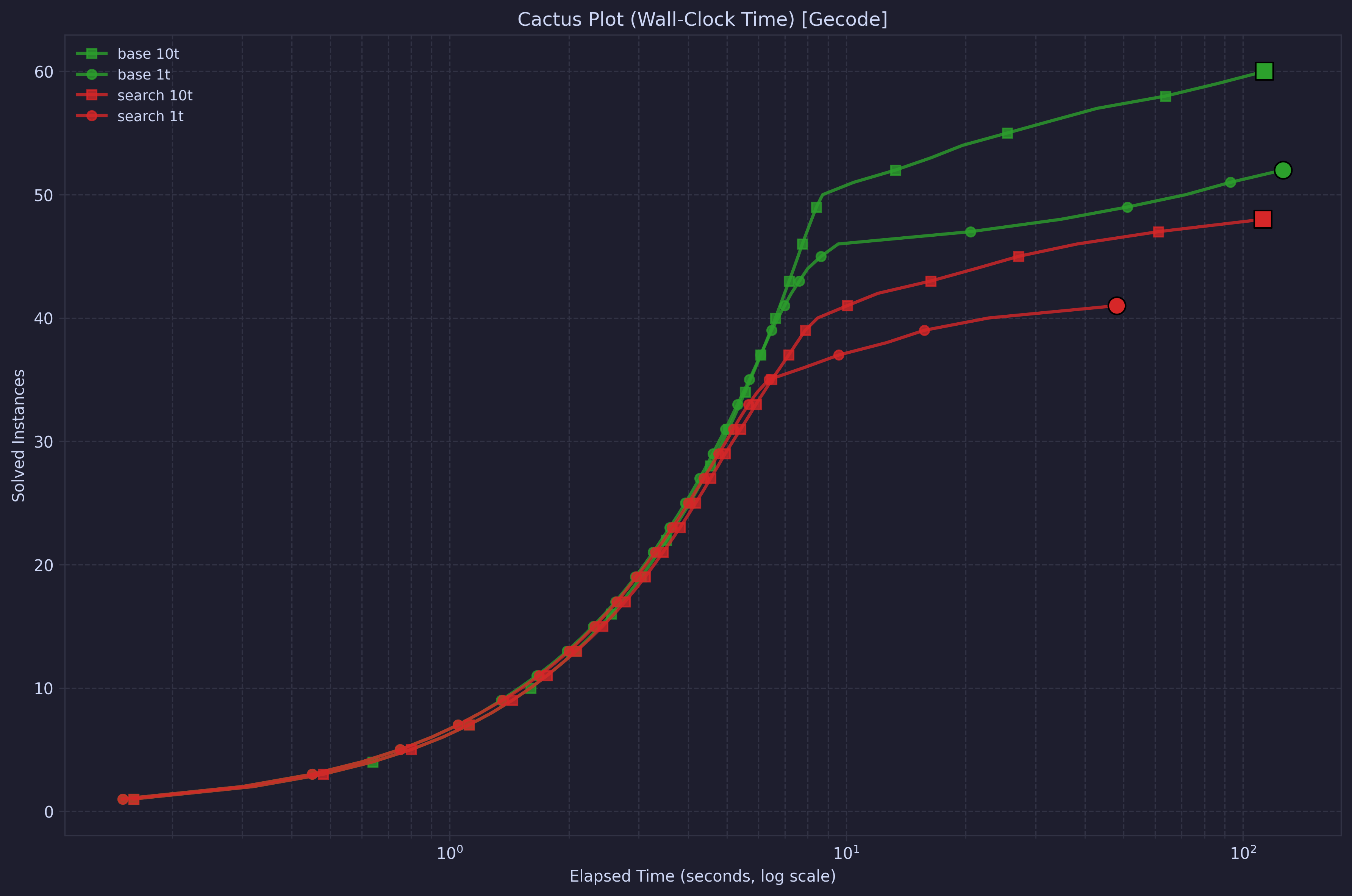
It is worth experimenting with search heuristics, even if they don’t always pan out. In a previous model for a similar problem a similar idea was good, but here it was worse than the automatic heuristics.
Summary
The above model shows how developing a model for a realistic problem can proceed. It will often not be as straightforward as this, but with the right view-point and a judicious use of extra variables many constraints are often natural to express. Doing the right experiments, and letting the choice of solver be data-driven is also very important.
The model here is as mentioned for a simplified version of many real-world rotating workforce scheduling problems. There is no optimization, while normally the goal is to optimize some parameter of the schedule. As for the data-model, it is common to not just have a set few different work types but instead to have custom and varied shifts with different start and end times. With that, there will be issues such as the total amount of work per week, resting times between work, ensuring enough rest over an off weekend, and so on. Even more important is to also take into account wishes and requests from the staff. Without their input, it is hard to make a schedule that will be appreciated.
Footnotes
-
The model here is partially inspired by the model in “Solver Independent Rotating Workforce Scheduling” by Musliu, Schutt, and Stuckey published at CPAIOR 2018. The specific constraints used are custom, and were originally developed for and published as a poster at Stockholm Optimization Days 2022 by me. ↩
-
It’s important to note that the
Shiftsare the first elements fromShiftsAndOff. This means that when defining arrays of matrices that only index onShifts, these start at 1, which ensures that there is no extra conversions needed. It would also be possible to defineShiftsas an enum, and then add a new enumenum ShiftsAndOff = S(Shifts) ++ { Off };, where the Off could go on either side. ↩ -
The regular constraint was introduced in “A Regular Language Membership Constraint for Finite Sequences of Variables” by Gilles Pesant at CP 2004. ↩
-
The original paper used Deterministic Finite Automata only, but as I noted in my licentiate thesis, the algorithm works also for Nondeterministic Finite Automata. ↩
-
Equivalently, one could have defined auxiliary variables
working_daysthat are the inverse ofoff_days, and usedsliding_sum(0, 5, 6, working_days)to indicate that a maximum of 5 days are spent working in a subsequence of length 6. ↩