Solving LinkedIn Queens using MiniZinc DRAFT

2025-06-19 • 13 min read •

Constraint programming MiniZinc models games

Hillel Wayne wrote about solving the LinkedIn Queens problem with SMT in his Computer Things newsletter. This was in turn inspired by Ryan Berger’s post Using SAT to Get the World Record on LinkedIn’s Queens that solves the same problem using a SAT solver.

Not to be outdone, this post describes how to use MiniZinc to solve the problem in what I think is a more readable and natural expression of the model than either SAT or SMT. As always, YMMV and what is natural and clear to one person is opaque and weird to someone else.

The Game

The basic game is somewhat similar to the classical N-Queens puzzle. The goal is to place $n$ queens on a $n\times n$ cheesboard. The two main differences are

The rules for attacking are a hybrid of chess pieces. A queen attacks any square on the same row or column (like a Rook), and any immediately adjacent square (like a King). The model will enforce these constraints separately.
There are $n$ connected areas with different colors, and there should be one Queen in each area.

Here is the example that both Ryan Berger and Hillel Wayne used.

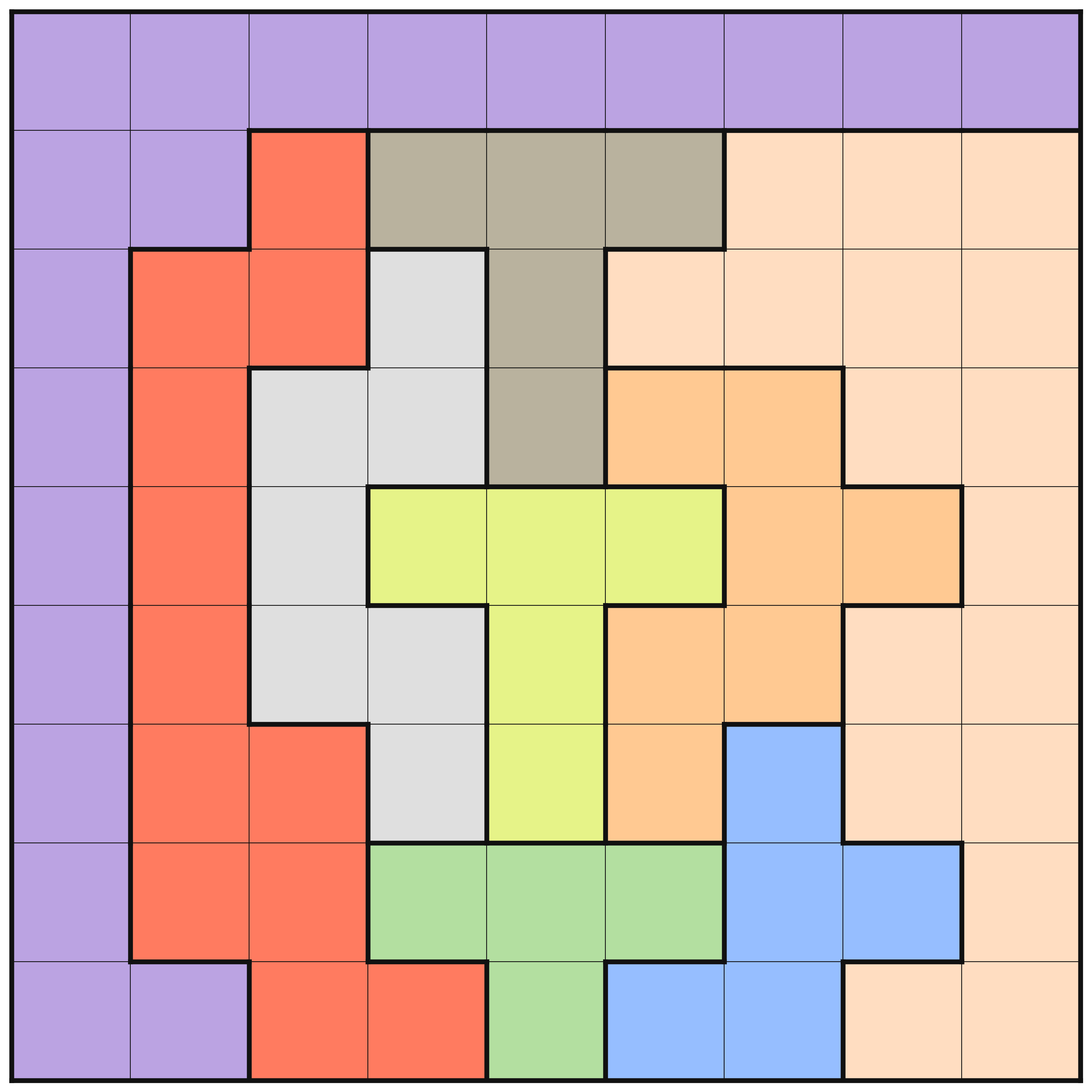
The image above shows the puzzle board for a $9\times 9$ instance, along with its unique solution.

MiniZinc

We will use the constraint modelling language MiniZinc. It is a language designed for expressing combinatorial optimization problems, not a general programming language. A constraint modelling language is specifically geared towards expressing models clearly, and will help show the essential aspects. In addition, MiniZinc can be used with many different constraint programming solvers and with other types of solvers as well such as Mixed Integer Programming solvers.

To try the model yourself, download the MiniZinc IDE which comes bundled with several solvers. This model was developed and tested with version 2.9.2. For a full introduction to MiniZinc, see the [MiniZinc Handbook](http://www.minizinc.org/doc-2.2.1/en/index .html).

The MiniZinc model

Let’s dive into how LinkedIn Queens can be modeled using MiniZinc. We will divide it up into four parts: the data, the variables, the constraints, and the search and output

Representing an instance

Each puzzle needs an input that specifies it. Here, we will use the fact that MiniZinc allows us to specify values in the main .mzn file that are unbound, and then later bind them in a data file .dzn.

% Size of board
int: n;
set of int: N = 1..n;

% set of colors
enum Colors;

% The colors on the boards defining the regions
array[N, N] of Colors: board;

We let n represent the size of the side of the board, and this is one of the unbound variables that are defined in a separate file. The set of integers N is constructed based on this value. Note that in MiniZinc it is common to use 1-based indexing for arrays. The enum Colors represents all the colors in a specific problem, and the board will be the set of colored areas.

Here is the data-file for the above puzzle, where the colors have been given somewhat cryptic names so that they have unique first letters. The reason that single letter names are used is to make the presentation easier to read.

n = 9;

Colors = {P, O, B, G, W, R, Y, S, L};

board = [|
  P, P, P, P, P, P, P, P, P | 
  P, P, R, S, S, S, L, L, L | 
  P, R, R, W, S, L, L, L, L | 
  P, R, W, W, S, O, O, L, L | 
  P, R, W, Y, Y, Y, O, O, L | 
  P, R, W, W, Y, O, O, L, L | 
  P, R, R, W, Y, O, B, L, L | 
  P, R, R, G, G, G, B, B, L | 
  P, P, R, R, G, B, B, L, L | 
|];

In the above data file, the side length n is specified to 9, the Colors are Purple, Orange, Blue, Green, White, Red, Yellow, Slate, and Lilac and the board is set to represent the layout of the instance.

The variables

Central to any type of combinatorial optimization modelling is deciding on the variables to use, sometimes called the viewpoint. In many cases, there are multiple ways to specify the variables that have their own benefits and drawbacks. For example, an immediate option is to use a matrix of $n\times n$ Boolean variables, where true represents that a Queen is placed in that position.

Here, we will instead use a classic trick for modelling N-Queens, by having $n$ variables, one for each row, with a domain that specifies in which column the Queen for that row is. This viewpoint has several benefits

The right number of queens is guaranteed
Exactly one queen per row is guaranteed
Makes other constraints straightforward

In MiniZinc, the variables are declared like this, an array of N variables that each can take a value in N.

array[N] of var N: queens;

The constraints

There are many types of constraints that can be added in MiniZinc, the reference manual lists them all. What is needed for the LinkedIn Queens problems are simple arithmetic constraints, the all_different constraint, and looking up values in an array with a variable index.

First of all, we need to make sure that there is a single queen in each column. This is done using the all_different constraint, which ensures that all the values take different values.

% Each queen is in a different column
constraint all_different(queens);

For the king-attacks, we need to make sure that two queens are never next to each other. This could only happen for two queens in adjacent rows, and the way we make sure they are not next to each other is to ensure the absolute difference between the columns for two adjacent rows is more than one.

% There are no queens directly adjacent to each other.
constraint forall (r in 1..n-1) (
    abs(queens[r] - queens[r+1]) > 1
);

The forall construction looks like a loop, but it is syntactic sugar that represents a conjunction of Booleans for an array. The explicit construction would be a call to the predicate forall using an array comprehension forall([abs(queens[r] - queens[r+1]) > 1 | r in 1..n-1]). This would in turn be the same as the logical formula

\wedge_{r=1}^{n-1}\,|\mathrm{queens}_r - \mathrm{queens}_{r+1}|>1

Finally, we need to make sure that each area gets its own queen. Here, we will use the array look up, where the expression board[1, queens[1]] will give us the color that the queen in row 1 is placed at. Using the same syntactic sugar as for forall, we can get all the colors of all the queens, and enforce an all_different constraint over the colors. Since the number of colors is the same as the number of queens, this means that every color will be used exactly once.

% Each queen is in a different color area
constraint all_different (i in N) (
    board[i, queens[i]]
);

Search and output

Using the solve satisfy; statement tells MiniZinc that it should find a satisfying solution. Here we give no search heuristic, so the solver is free to do whatever it wants. The output statement takes an array of strings and prints them. Here the concat function is used which takes an array of strings and concatenates them, and the ++ operator which concatenates two strings. This builds up the board, with squares with queens represented with q.

solve satisfy;

output [
    "Board:\n",
    concat(r in N) (
        concat(c in N) (
          if fix(queens[r]) == c then 
              "q" 
          else 
              show(board[r,c]) 
          endif  
        ) ++ "\n"
    ),
];

The full program

For testing, you can get the full MiniZinc model as well as the instance. Opening both in the MiniZinc IDE will give UI access to solving with all the different solvers in MiniZinc.

Solving the instance

We’ve seen the full model now, but the question is, can the system solve it? Yes, this type of problem is quite easy to solve regardless of which type of combinatorial optimization solver one uses.

Gecode

Solving using the built-in standard Gecode solver which is a traditional constraint programming solver gives the following output on the command line.

$ minizinc --statistics linkedin-queens.mzn instance.dzn
% Generated FlatZinc statistics:
%%%mzn-stat: paths=0
%%%mzn-stat: flatIntVars=33
%%%mzn-stat: flatIntConstraints=27
%%%mzn-stat: method="satisfy"
%%%mzn-stat: flatTime=0.197035
%%%mzn-stat-end
Board:
qPPPPPPPP
PPRSSqLLL
PRRWSLLLq
PRqWSOOLL
PRWYYYOqL
PRWWqOOLL
PqRWYOBLL
PRRqGGBBL
PPRRGBqLL
----------
%%%mzn-stat: initTime=0.00596508
%%%mzn-stat: solveTime=0.00172683
%%%mzn-stat: solutions=1
%%%mzn-stat: variables=34
%%%mzn-stat: propagators=26
%%%mzn-stat: propagations=2442
%%%mzn-stat: nodes=62
%%%mzn-stat: failures=29
%%%mzn-stat: restarts=0
%%%mzn-stat: peakDepth=11
%%%mzn-stat-end
%%%mzn-stat: nSolutions=1
%%%mzn-stat-end

Solving takes a few milliseconds (the solveTime statistic), and explores a search tree with just 29 failures before the solution is found. Before the solution, the flatTime statistic tells us the time it took for MiniZinc to convert the problem into a simpler representation that the solver uses which is around 200 milliseconds.

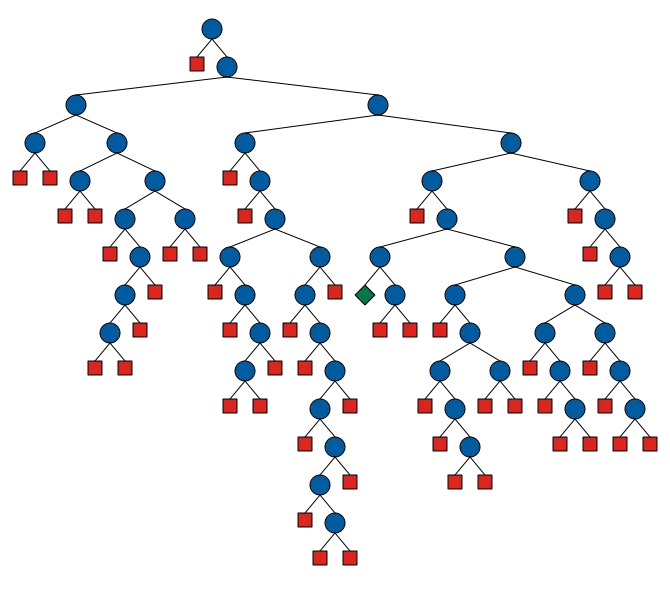
Gecode also has a built-in visual search tool called Gist. This can be used to visualize the full search tree, which is shown here. The blue circles are interior nodes, the red squares are failures, and the green rhombus is the single solution.

OR-Tools CP-SAT

The OR-Tools CP-SAT solver is a Lazy Clause Generation constraint programming solver with a powerful portfolio of various techniques, including a built-in MIP solver, Large Neighborhood Search, and local search. The portfolio is very useful for finding good solutions to optimization problems using multiple threads. The current problem is quite easy though, but it is still interesting to see that MiniZinc allows us to test different solvers.

The only real difference in solving the problem using CP-SAT instead is that a --solver argument is supplied on the command line to select the right solver. CP-SAT comes built-in with the MiniZinc distribution, so it is ready to go.

$ minizinc --solver ortools --statistics linkedin-queens.mzn instance.dzn
% Generated FlatZinc statistics:
%%%mzn-stat: paths=0
%%%mzn-stat: flatIntVars=33
%%%mzn-stat: flatIntConstraints=27
%%%mzn-stat: method="satisfy"
%%%mzn-stat: flatTime=0.223653
%%%mzn-stat-end
Board:
qPPPPPPPP
PPRSSqLLL
PRRWSLLLq
PRqWSOOLL
PRWYYYOqL
PRWWqOOLL
PqRWYOBLL
PRRqGGBBL
PPRRGBqLL
----------
==========
%%%mzn-stat: objective=0
%%%mzn-stat: objectiveBound=0
%%%mzn-stat: boolVariables=86
%%%mzn-stat: failures=0
%%%mzn-stat: propagations=86
%%%mzn-stat: solveTime=0.015447
%%%mzn-stat: nSolutions=1
%%%mzn-stat-end

The same solution is found in a similar amount of time, but the pre-processing that CP-SAT does means that the solution is found without any failures in the search.

The HiGHS MIP Solver

As mentioned, MiniZinc is not limited to just using constraint programming solvers, it can also be used with other types of solvers. One such built-in solver is the HiGHS MIP solver. The model stays the same, but MiniZinc will translate it into a different representation when solving. Again, the only difference for the user is supplying a different solver name.

$ minizinc --solver highs --statistics linkedin-queens.mzn instance.dzn
% Generated FlatZinc statistics:
%%%mzn-stat: paths=0
%%%mzn-stat: flatIntVars=202
%%%mzn-stat: flatIntConstraints=124
%%%mzn-stat: evaluatedReifiedConstraints=8
%%%mzn-stat: method="satisfy"
%%%mzn-stat: flatTime=0.146041
%%%mzn-stat-end
%%%mzn-stat: nodes=1
%%%mzn-stat: solveTime=0.0730
%%%mzn-stat-end
Board:
qPPPPPPPP
PPRSSqLLL
PRRWSLLLq
PRqWSOOLL
PRWYYYOqL
PRWWqOOLL
PqRWYOBLL
PRRqGGBBL
PPRRGBqLL
----------
%%%mzn-stat: nodes=1
%%%mzn-stat: solveTime=0.0730
%%%mzn-stat-end
%%%mzn-stat: nSolutions=1
%%%mzn-stat-end

Here, the solve-time is also very quick and uses just a single node so it is found without search, and the the same solution is found.

Using more pre-processing

As we could see, both CP-SAT and HiGHS could solve the problem without search. We’ve so far used MiniZinc with the standard settings, but there are alternatives that use pre-processing before sending the problem to the underlying solver.

The -O5 option will do all the pre-processing that MiniZinc can, and includes something called domain shaving or singleton arc consistency. This means that MiniZinc will test each value for each variable, and if assigning that value to that variable would directly lead to a failure, then that possibility is removed from the problem. Let’s try it out with the standard Gecode solver that does not do any pre-processing in particular.

$ minizinc -O5 --statistics linkedin-queens.mzn instance.dzn
% Generated FlatZinc statistics:
%%%mzn-stat: paths=34
%%%mzn-stat: flatIntConstraints=1
%%%mzn-stat: method="satisfy"
%%%mzn-stat: flatTime=0.317172
%%%mzn-stat-end
Board:
qPPPPPPPP
PPRSSqLLL
PRRWSLLLq
PRqWSOOLL
PRWYYYOqL
PRWWqOOLL
PqRWYOBLL
PRRqGGBBL
PPRRGBqLL
----------
%%%mzn-stat: initTime=0.000132292
%%%mzn-stat: solveTime=3.1e-05
%%%mzn-stat: solutions=1
%%%mzn-stat: variables=9
%%%mzn-stat: propagators=0
%%%mzn-stat: propagations=2
%%%mzn-stat: nodes=1
%%%mzn-stat: failures=0
%%%mzn-stat: restarts=0
%%%mzn-stat: peakDepth=0
%%%mzn-stat-end
%%%mzn-stat: nSolutions=1
%%%mzn-stat-end

The flattening time has increased, and from the statistics we can see that Gecode could now solve the problem without any search at all.

Using -O5 is a large hammer, and is not always useful in practice, but it is worth knowing about since it is sometimes very useful.

Summary

The LinkedIn Queens problem is a small, fun, and simple puzzle that is designed to be easy to do in a short amount of time. As such, it is not surprising at all that using any kind of combinatorial optimization solver will solve the given problem instances quickly. But as with all combinatorial problems, increasing the size of the problem will also increase the difficulty, and it would be interesting to try SAT vs SMT vs CP on a set of larger instances.

The main point I would like to make with this post, is that I think that MiniZinc has two main features that make it attractive for modelling these types of problems.

Clarity and readability of models
The ability to experiment with different solvers

While the SAT and SMT models are not very difficult to understand for this problem, for larger and more complicated problems I think that the differences start to add up.

Solving LinkedIn Queens using MiniZinc

Menu