The paper The Work Task Variation Problem by Mikael Z. Lagerkvist and Magnus Rattfeldt was presented at the 31st International Conference on Principles and Practice of Constraint Programming (CP 2025) in Glasgow, Scotland. This post summarizes the paper and provides some context.

The paper is available on my research page and the benchmark instances and MiniZinc model are available on GitHub.

What is the Work Task Variation Problem?#

Employee scheduling is a well-studied area, but most research focuses on generating feasible schedules that meet business demands. However, the quality of an individual’s shift, especially regarding task variety and ergonomics, is often overlooked. This can lead to fatigue, reduced productivity, and even safety risks from repetitive tasks.

The Work Task Variation (WTV) problem addresses this gap. It’s a post-processing problem that takes an existing schedule and improves it by rearranging tasks to create better work patterns for employees, without changing the overall staffing levels. This is a problem we encountered in practice at Optischedule, where we needed a way to quickly improve schedules for retail clients to make them more ergonomic for their staff.

The Work Task Variation Problem#

The WTV problem starts with a complete schedule where workers are assigned to time slots. The goal is to rearrange the tasks within those slots to improve the variation of work for each employee. The main objective is to avoid situations where a worker performs the same task for too long or switches between tasks too frequently.

For example, consider the three different shifts below for a single worker with tasks T for till, S for store, and W for warehouse. The first shift is bad because the person working has to run around all the time. The second shift is bad because the time at the till is too long for one go. The third shift is good, because the time at the till is split up, but not fragmented. The long stretch in the warehouse is also acceptable, as the rules vary with the task type.

This is important in industries like retail (long hours at a till), logistics (repetitive picking/packing), and manufacturing (assembly line work). Solving the WTV problem provides a way to make schedules more sustainable and pleasant for employees.

The key constraints are:

• The time spans for each worker are fixed.
• The total number of workers assigned to each task in any given time slot remains the same.
• Some specific assignments can be fixed and must be respected (like lunch breaks and similar).

Planning context#

In the types of setups we have encountered, it is common for planners to iteratively receive schedules from a planning system and ask for adjustments. The planning system generates these schedules based on some business data and the availability of employees.

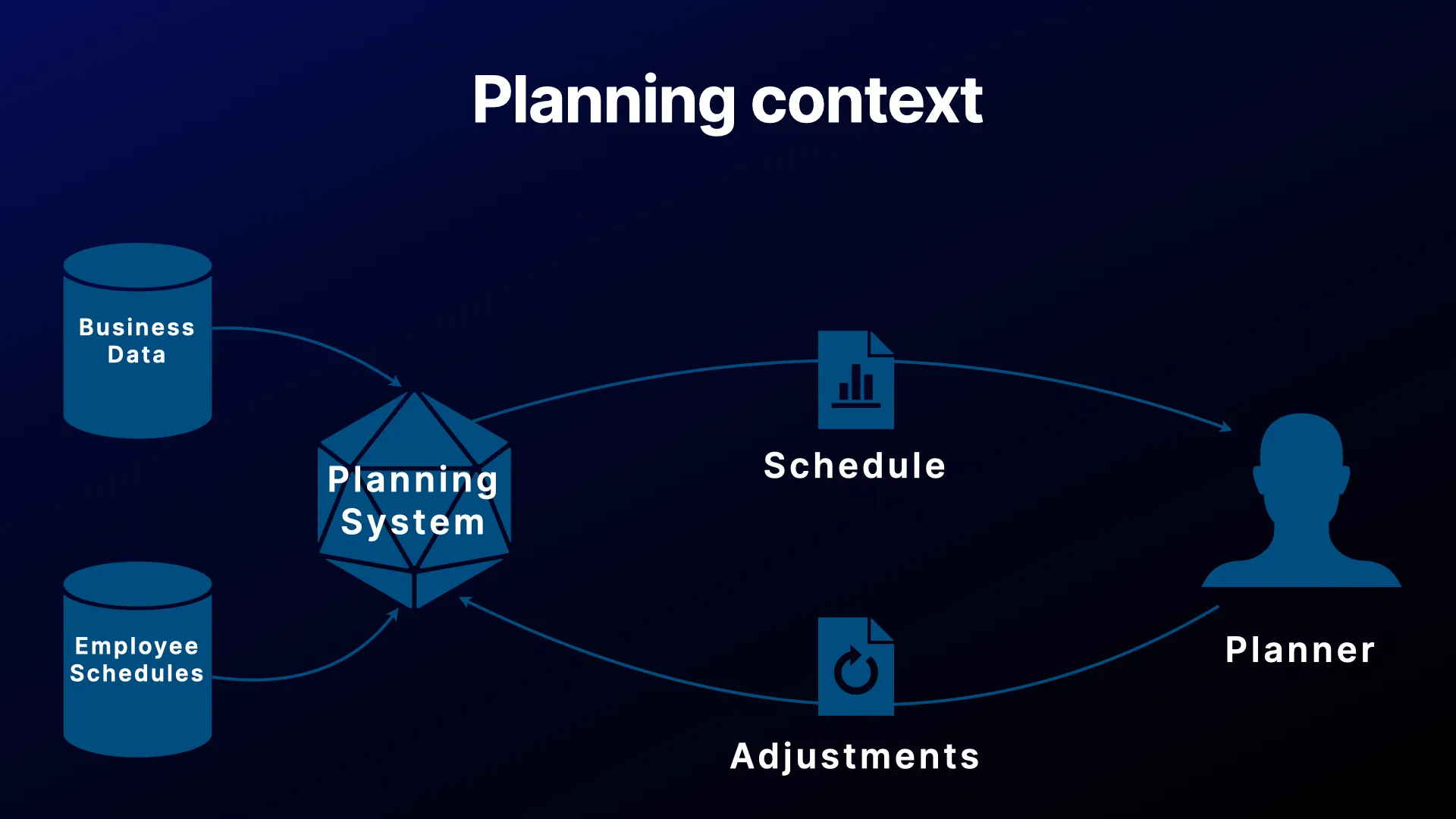
However, as mentioned, these plans often lack suitable task variation. The idea is to introduce a WTV solver as a post-processing step to improve the automatically generated schedules.

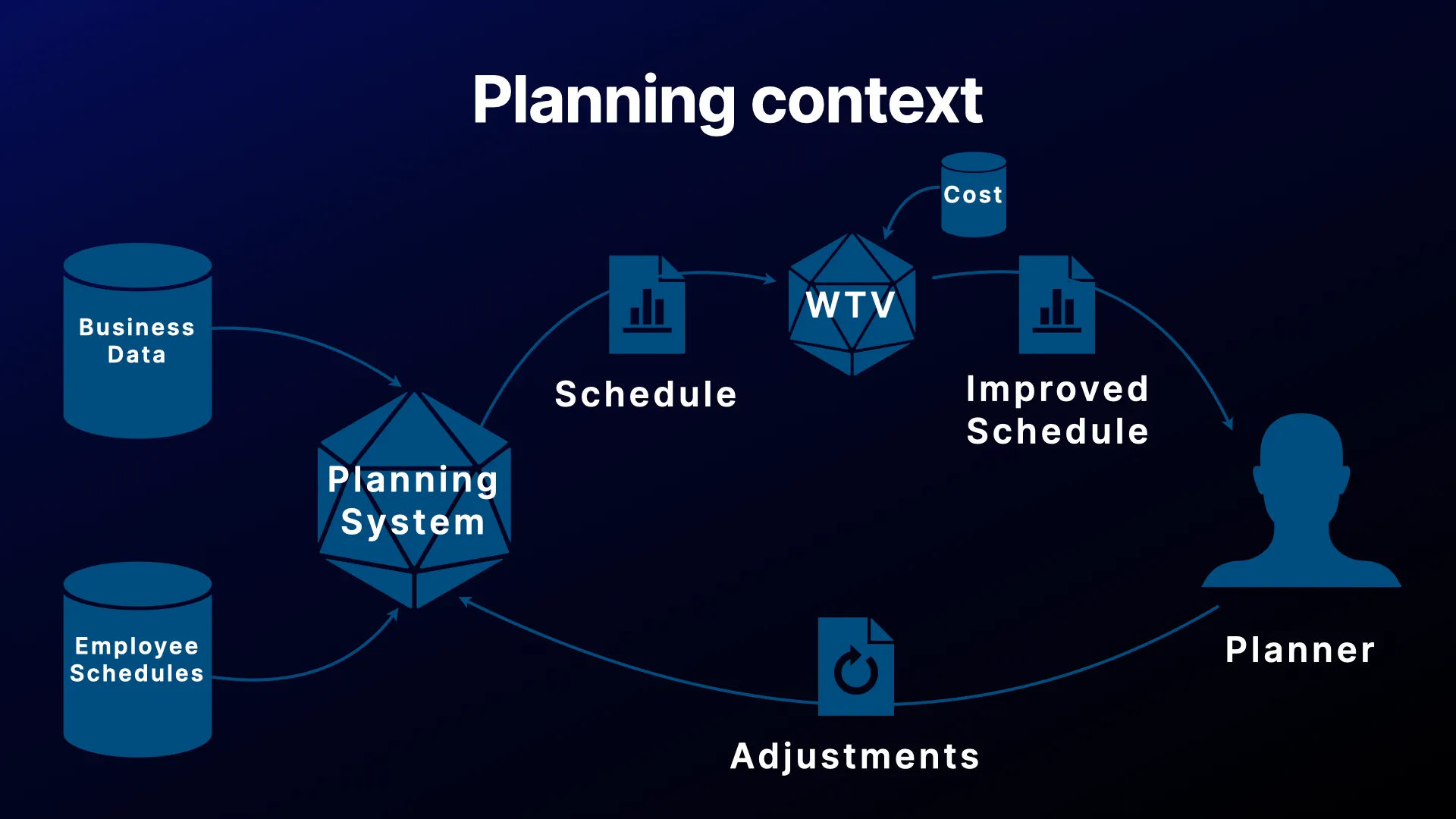
Since the system operates in an interactive loop, a WTV solver should not add too much additional time for obtaining good solutions.

RosterLogic Variation: A CBLS-inspired Solver#

To solve the WTV problem in an interactive setting, we developed RosterLogic Variation, a solver inspired by Constraint-Based Local Search (CBLS). Since we start with a full, valid schedule, a local search approach that iteratively improves the schedule is a natural fit. The solver is designed to be fast, making it suitable for a human planner who needs quick results.

The solver uses several techniques:

• Efficient State Representation: The schedule is stored in a compact matrix. The run-length encoding is maintained as an invariant, and moves can be evaluated using simulation.
• Fast and smart moves: We define several types of moves to explore neighboring solutions. Among these, swaps of length 1 or more between workers are the main moves used. In addition, Pattern Moves are designed to create known good patterns of tasks.
• Search: We use a portfolio of search algorithms, including steepest descent, tabu search, and simulated annealing, running in parallel to explore the search space effectively.

This solver has been successfully used in production environments for retail scheduling.

A MiniZinc Model and Benchmarks#

To help the research community engage with the WTV problem, we also created a formal MiniZinc model. This model precisely defines the problem and allows other researchers to experiment with different solvers. The model works over a set of declarations that are defined in a data-file.

enum Resources;
enum Activities;

enum ActivitiesOrNone = A(Activities) ++ { None };

int: slots;
set of int: Slots = 1..slots;
set of int: SlotsAndZero = 0..slots;

array[Activities, Slots] of 0..card(Resources): requirements;

array[Resources, Slots] of opt ActivitiesOrNone: fixed;

array[Activities, SlotsAndZero] of int: activity_run_cost;
array[Activities, SlotsAndZero] of int: activity_frequency_cost;

The core components are the Resources (the employees), the types of Activities, and the Slots to plan in. Not shown is that the run cost and the requirements are both extended to be defined over ActivitiesOrNone.

The core of the model consists of variables for the schedule and the lengths of runs of similar tasks. The lengths of runs are needed in order to compute the cost of a schedule for both run lengths and frequencies of task runs.

% The actual schedule, what activities are done when for each resource
array[Resources, Slots] of var ActivitiesOrNone: schedule;

% Markers for when runs end
array[Resources, Slots] of var bool: run_end;

% Length for each run at the current slot from the current run's start
array[Resources, Slots] of var SlotsAndZero: run_length;

% Cost for each run at the end of a run with zero cost in the middle of runs
array[Resources, Slots] of var int: run_cost;

% Cost for number of runs of each activity per resource
array[Resources, Activities] of var int: frequency_cost;

% The total cost of runs
var int: cost = sum(run_cost) + sum(frequency_cost);

The constraints for these variables are the following. They are divided up into the constraints for the rules and structure of the problem, and the calculation of costs.

% Constraints for structure
%

% All shifts are only Activities (that is, not None) and surrounded with None
constraint forall (r in Resources) (
  regular(schedule[r, ..], "None* [^None]* None*")
);

% Always respect the requirements for each slot (column in the schedule)
constraint forall (s in Slots) (
  global_cardinality(schedule[.., s], ActivitiesOrNone, extended_requirements[.., s])
);

% Always respect the fixed requirements
constraint forall (r in Resources, s in Slots where occurs(fixed[r, s])) (
  schedule[r, s] = deopt(fixed[r, s])
);

% Mark when runs end
constraint forall (r in Resources, s in Slots) (
  if s = slots then
      run_end[r, s] = true
  else
      run_end[r, s] = (schedule[r, s] != schedule[r, s+1])
  endif
);

% Count length of runs
constraint forall (r in Resources, s in Slots) (
  if s = 1 / run_end[r, s-1] then
      run_length[r, s] = 1
  else
      run_length[r, s] = run_length[r, s-1] + 1
  endif
);


% Constraints for calculating costs
%

% Count run costs
constraint forall (r in Resources, s in Slots) (
  if run_end[r, s] then
      run_cost[r, s] = extended_activity_run_cost[schedule[r, s], run_length[r, s]]
  else
      run_cost[r, s] = 0
  endif
);

% Count frequency costs
constraint forall (r in Resources, a in Activities) (
  let {
      var int: activity_run_count = count(s in Slots) (
          run_end[r, s] / schedule[r, s] = A(a)
      )
  } in
  frequency_cost[r, a] = activity_frequency_cost[a, activity_run_count]
);

The full model is available for experimentation. Alongside the model, we have generated and released a public dataset of 400 realistic benchmark instances. These instances mimic the characteristics of real-world retail scheduling problems.

Our experiments show that for many common cases (e.g., 15-minute planning intervals), modern CP solvers like Google OR-Tools’ CP-SAT are becoming competitive with our specialized RosterLogic Variation solver. However, for finer-grained schedules (e.g., 5-minute intervals), our custom solver still provides superior solutions within an interactive time frame.

The problem was also used in the 2025 MiniZinc Challenge

Conclusion#

The WTV problem is an important but often overlooked aspect of personnel scheduling. We hope that by formally defining the problem, providing a real-world solver, a MiniZinc model, and a set of benchmarks, we can encourage more research in this area. Improving task variation is a direct way to enhance worker well-being and create more sustainable and productive schedules.

The development of RosterLogic Variation shows that for specific industrial problems, a custom solver can be highly effective. At the same time, the rapid progress of general-purpose CP solvers is impressive, and they are catching up quickly.