Nmbr9 as a Constraint Programming Challenge

The abstract State Representation and Polyomino Placement for the Game Patchwork by Mikael Z. Lagerkvist is presented as a poster at the The 25th International Conference on Principles and Practice of Constraint Programming, CP2019 in Stamford, CT, USA. This post summarizes the abstract and gives some context on it.

The abstract is available on my research page.

What is Nmbr9 and why is it a challenge?

Nmbr9 is a fun solitaire game that can be played by multiple people simultaneously. The game mechanic uses polyomino placement, and after previous forays into pure polyomino placement and polyomino placements in games, Nmbr9 seemed like a natural place to continue. In particular, it has a very interesting open question which is what the maximum possible score is.

The model turned out to be quite a bit more complex than my previous polyomino placement models, and in the end the full game is way too complex to solve. The title of the paper, Nmbr9 as a Constraint Programming Challenge, is in the hope that someone else may become inspired and find better ways to model it.

Nmbr9 rules

Nmbr9 by Peter Wichmann is a solitaire puzzle game using polyominoes that can be played by multiple people at the same time. The goal of the game is to build layers of the polyominoes below according to a pre-defined but unknown shuffle, and to place polyominoes representing larger numbers higher up to score points.

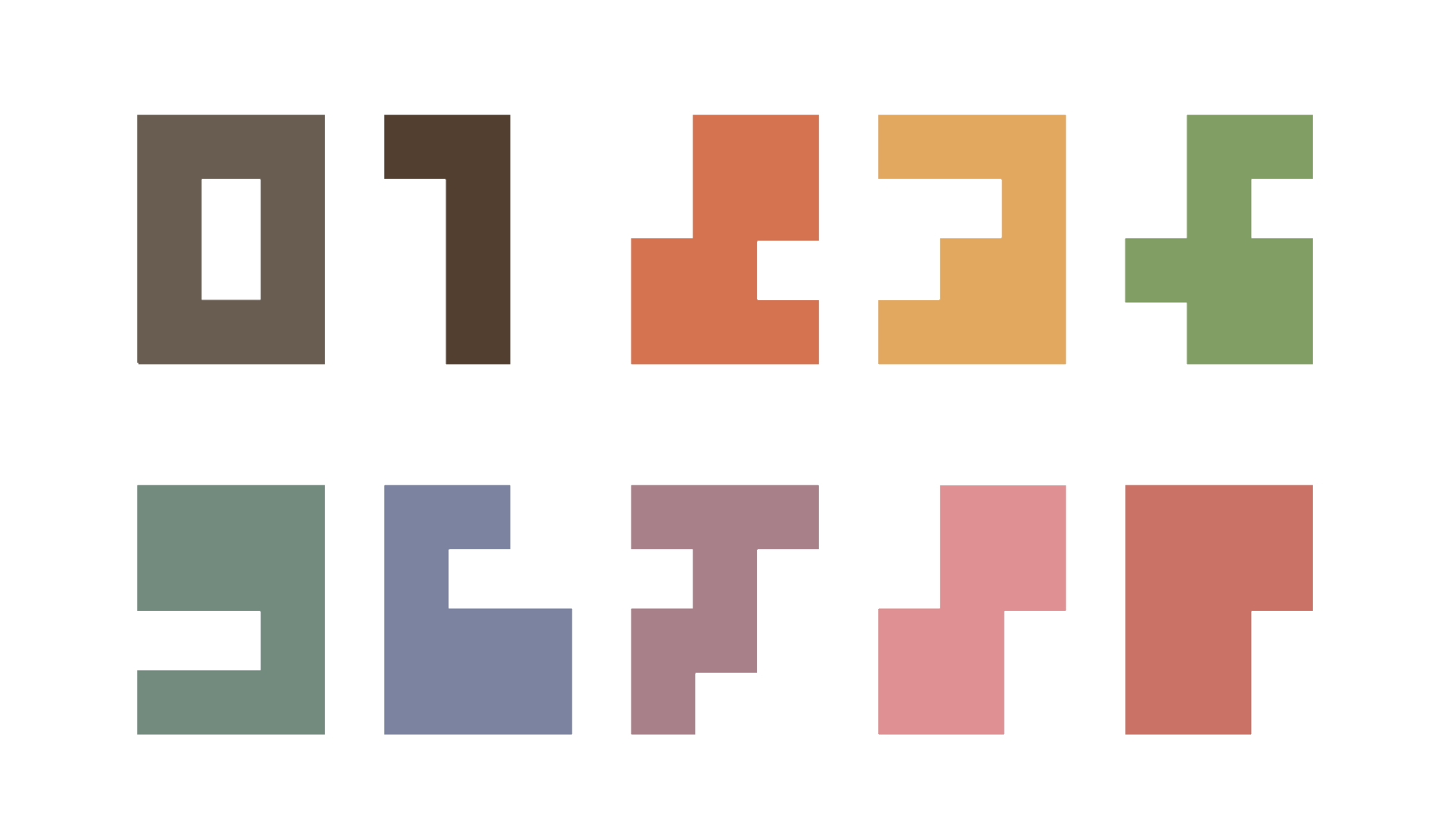
The game consists of two copies of the above tiles per number for each player. A common deck of 20 cards with the polyominoes are shuffled. When a card is drawn, each player takes the corresponding part and places it in their own area. Placements are done in levels, where the first level (level 1) is directly on the table, and level n is on top of level n-1.

Placement must always be done fully supported (level 1 is always fully supported, level n is supported by previously placed parts in level n-1). Each level must be fully 4-connected (i.e., not diagonally) after placement. The final requirement on placements is that when placing a part on top of other parts, it must be on top of at least two different parts. For example, if a 9-part is in level n, then an 8-part can not be placed in level n+1 resting solely on the 9-part.

When all cards have been drawn, the score is computed as the the sum of the value for parts times their level minus one. For example, an 8-part on level 3 is worth 16, while it is worth 0 on level 1.

Variants of Nmbr9

The base game is a single instance, and it is quite a large one at that. In order to have more instances and variants to try on, I defined variants of Nmbr9 according to the following scheme. A variant is denoted by T-m-c-k, with the following meaning

• T in {U,F,K} Whether the draft is unknown, free to choose, or known. The first corresponds to a quantified problem, where the draft is forall-quantified. The second models the question of the max possible score, while the last models the max possible score given a specific known shuffle.
• m The maximum value to use, from 0-9.
• c The number of available copies of each polyomino.
• k The number of cards in the deck to use, which can be at most m+1 times c.

With this taxonomy of variants, the standard game is U-9-2-20, where all available parts are used. F variants are interesting for answering the question of the top-score possible. K variants are interesting computationally because they represent a much simpler but still hard problem, and are also interesting recreationally given a finished game, where participants wonder how they compare to the best possible result for that particular shuffle.

At Board Game Geek, a forum thread on solving the standard F-9-2-20 instance has a top score of 229 points, using a total of 7 layers.

Constraint programming model

The constraint programming model used is based on the one for Patchwork. However, for patchwork several complicating features are added.

• There is no fixed boundary or tight upper limit on layers, which means an over-approximation is needed to be sure not to rule out solutions.
  
• Placements in layers means than many more regular placement constraints are needed than in Patchwork, making the model costlier to propagate.
• The rules for support and connectedness combined with order of placement for parts are quite intricate, and the presented model uses a lot of reification to model this.

The details of the model are described in the paper, but suffice to say that it is not really an effective model. In particular, setting up the standard problem on a 20 by 20 grid with 7 layers leads to a model with more than 2.5 million propagators, which is clearly not a reasonable amount.

Adding symmetry breaking constraints (ordering of similar parts, rotation of base layer), and implied constraints on the number of parts and area of each layer is very important to solve smaller problems.

Search strategy

Finding a good search strategy is hard, and especially when models are complicated leading to slow search. Some experimenting led me to the following heuristics:

• First branch on the order of parts in the deck. This is important because without this order, the before-relation between parts will not be set, leading to no propagation at all on the possible placements.
• Secondly, branching is done on the level of each part, without setting the placement. Setting the level of a part will ensure that the final score is known, if the placement is possible.
• Finally, parts are placed. At this point, the levels and order of parts is known, making propagation quite a bit stronger. A fixed variable ordering is used, spiralling out from the center to keep placements centered on the board. For each variable, the possible parts are tried before setting the place to empty.

I think that it would be possible to implement better ways to branch, probably by intermingling the above strategies. For now I have not found any smart way to do so. The spiralling static variable ordering was interesting to do, and using a static order for the variables when placing is suggested by the results for Patchwork.

Implementation

The implementation is done in C++17 and uses the Gecode constraint programming system. The implementation is available on GitHub.

One fun aspect is how K variants (a known deck) is implemented. The model can be run for this mode, and in that case an assignment with random value order for the deck variables is set as the first branching. This simulates a random drawing using the built-in capabilities of Gecode.

Reflections

I imagined that the full Nmbr9 problem would be quite complicated to solve, but the amount of reified constraints needed to implement the rules surprised me. I really hope that either I or someone else finds a better way to model this.